BAZI DOĞA OLAYLARI "DOĞAÜSTÜ" MÜ?

Tarihsel gerçekliği biraz kuşkulu da olsa din-bilim ilişkisini çok güzel anlatan bir anekdot vardır: Ünlü matematikçi ve astronom Pierre-Simon Laplace’ı (1749 – 1827) İmparator Napolyon ile tanıştırırlar. İmparator “Neden Satürn ve Uranüs’ün yörüngelerini tartıştığınız kitabınızda Tanrı’yı hiç anmıyorsunuz?” diye sorunca Laplace “Bu hipotez hiç gerekli olmadı” der[i]. 

Sanrım hepimiz doğadaki bazı güzellikleri görünce hayretler içinde “nasıl oluyor da bu kadar karmaşık ve güzel yapılar oluşuyor” deriz. Gördüklerimiz bize bir mucize gibi gizemli, inanılmaz ve adeta “doğaüstü” gibi gelir. Bir “rastlantı” olmadığı bellidir. Birçok kişi bu yapıları kendi dini inancına göre bir yaratılış mucizesi olarak yorumlar. Olayı bilimsel yöntemle inceleyip evrenin güzel dili olan matematiksel tabanını kavradığımızda ise “tabii böyle olmak zorunda, başka türlü olamaz ki” deriz. 

Bir an için bilimin henüz çevremizi aydınlatmadığı bir çağda olduğumuzu düşünelim. Güneş her gün doğup çevreyi aydınlatıp ısıtıyor. Ardından batıp bizi karanlıklar içinde gökyüzündeki küçük ışıklara bırakıyor. Kış gelince hava soğuyup kar yağıyor. Bir süre sonra hava ısınıp doğa uyanıyor; kuru dere yatakları akarsularla doluyor; bitkiler yeşeriyor; ağaçlar meyve veriyor. Günümüzde bu doğa olaylarının yerkürenin hareketleriyle oluştuğunu biliyoruz ve bize hiç de gizemli gelmiyor. İlköğrenim çağındaki çocuklarımıza kolayca öğretiyoruz. 

Pekiyi, artık her şeyi öğrendik mi? Doğada bizi şaşırtan, hayranlıkla izlediğimiz bir şey kalmadı mı? Kuşkusuz pek çok şey var; iyi ki var. Hatta bunlar giderek artıyor. Bu yazıda bizi hayran bırakan konuların altında matematik ve doğa bilimlerinin açıkladığı “gizlerin” olduğu konusunda iki örnek vermek istiyorum: Kar kristalleri ve spiral yapılar. Bu yapıların ayrıntılı incelemesi matematiksel modeller ve onlar üzerine geliştirilen bilgisayar yazılımları ile yapılıyor. Kuşkusuz dergimiz bu amaç için uygun değil. Ama sanırız aşağıdaki örneklerle bir fikir verilebilir ve temel fikir açıklanabilir.

KAR KRİSTALLERİNİN BÜYÜLEYİCİ GÜZELLİĞİ

Kar kristallerini gözlemek oldukça iyi donanıma sahip olmayanlar için çok da kolay değildir. Ama hepimiz kar kristallerinin oldukça farklı biçimlerde çok güzel simetrik şekiller oluşturduğunu biliriz[ii]. Örneğin J. Kepler (1571 – 1630) ve R. Descartes (1596 – 1650) de bu altıgen simetrinin büyüsüne kapılan ünlü bilim insanları arasındadır. Çeşitli hipotezler bir yana, olayın kesin çözümü atom, molekül, kristal yapıları konularında yeterli teknolojik olanaklara kavuşmamız ve bilgi birikimi ile sağlandı. 

Kar tanesi, su buharının (yağmur damlasının değil) donması ile oluşur. Su buharı molekülleri (H₂O) donduklarında Şekil - 1’de gösterildiği gibi altıgen (hexagonal) yapılar oluşturur.

Şekil - 1 Altıgen Oluşumu

Kristaller gökyüzünde izledikleri yola, geçtikleri sıcaklık katmanlarına ve bulutlara bağlı olarak şekil alır ve büyür (Şekil – 2)[iii].

Şekil - 2 Sıcaklık - Nem

Sıcaklık ve nem koşulları Düzlemsel Yıldızlar oluşmasına uygunsa Şekil - 3’de görüldüğü gibi bizleri hayran bırakan kar kristalleri oluşur. Bu şekillerin birbirinden farklı olması da ayrıca dikkat çekicidir. Bunun nedeni de gökyüzünde uçuşan her bir kar tanesinin farklı bir yol izleyip farklı sıcaklık ve nem koşullarıyla karşılaşmasıdır. Örneğin ilk altıgenin oluşmasını izleyen aşamaları düşünelim. Bunlara yine altıgenler eklenecek, ama altıgenlerin boyutları farklı olabilecektir. İkinci aşamada Şekil‑3’ün üst sırasında görüldüğü gibi düzgün altıgenler veya alt sıradaki gibi uzun altıgenler oluşabilir. Üçüncü,  dördüncü aşama için de yine benzer olasılıklar kar kristallerinde hayranlıkla izlediğimiz birbirinden farklı, ama hepsi altıgen simetrik desenleri yaratır.

Şekil - 3 Kar Kristalleri

İşte hayranlık duyduğumuz kar kristalleri kabaca böyle oluşuyor. Farklı sıcaklık ve nem koşulları altında altıgen yapıların bilgisayar modelleri kullanarak farklı biçimler almasının ayrıntılı incelemesi bu yazının kapsamı dışında kalıyor. 

KUSURSUZ SPİRALLER

Bir başka örnek olarak deniz kabuklularından, mercanlara, çiçek göbeklerine, enginara, lahanaya, çam kozalağına hatta galaksimize kadar gözlediğimiz kusursuz spirali ele alalım (Şekil - 4).

Şekil - 4

Bu şeklin de temeli biyolojik yapılardaki büyümedir ve ilginç bir matematiksel diziye, Fibonacci dizisine dayanır. 1 ve 2 ile başlayıp kendinden önce gelen iki sayının toplamı ile sonsuza dek uzanan tam sayılar dizisini düşünelim: 1, 2, 3, 5, 8, 13, 21, 34, 55… . Leonardo Fibonacci (1175 – 1250) bu diziyi tavşanların üremesine dayanan bir örnekle açıkladıysa[iv] da olay yukarıda belirttiğimiz gibi doğadaki temel büyüme modellerinden biridir ve birçok biyolojik büyümede gözlenebilir. 

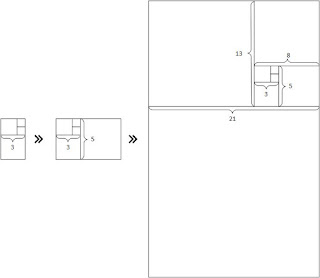
Yukarıdaki Fibonacci yaklaşımını kullanarak birbiri üzerine öyle kareler çizelim ki yeni karenin kenar uzunluğu kendinden önce çizdiğimiz iki karenin kenarlarının toplamı olsun (Şekil - 5).

Şekil - 5

Giderek büyüyen bu karelerin köşelerini birleştiren eğri kusursuz spiralimizi oluşturacaktır (Şekil – 6):

Şekil - 6

Bu temel geometrik şekli çeşitli biçimlerde kopyalayarak doğada gördüğümüz çoklu spiralleri oluşturabiliriz (Şekil - 7).

Şekil - 7

Fibonacci dizisini bazı yaprakların dizilmesinde gözleyebiliriz. Fibonacci dizisinde art arda gelen sayıların oranlarını aldığımızda sonucun irrasyonel bir sayı olan ϕ’ye (1,617647…) yakınsadığını görürüz (Çizelge – 1)[v].

Bir tomurcuktan çıkan yapraklarla bitkinin büyüdüğünü düşünelim. Eğer 360⁰’yi 2, 3, 4 gibi bir tam sayıya bölerek yapraklar arasındaki açıyı elde eder ve yaprakları bu açı ile yerleştirirsek belirli bir süre sonra yapraklar üst üste gelecek ve üstteki yaprak alttakinin ışığını kapatacaktır. Örneğin Şekil – 8’de 180⁰ açı ile yerleşmiş yapraklardan 3’ncüsü; 120⁰ açı ile yerleşmiş yapraklardan 4’cüsü ve 90⁰ açı ile yerleşmiş yapraklardan 5’incisi, 1nci yaprağın gölgesinde kalıyor.

Şekil - 8

Oysa 360⁰’yi irrasyonel bir sayıya bölüp bulunan açı ile yapraklar dizilirse bu sakınca önlenecektir. Evet, tahmin ettiğiniz gibi güzel spiral oluşturan bitkiler için bu sayı ϕ’dir. Şekil –  9’da 222,5⁰ açı ile (360/1.617647…≈225,5⁰) dizilen yapraklar görülüyor.

Şekil - 9

Kuşkusuz bitki açıları ölçerek yaprak çıkartmaz. Bitkinin büyüme hormonunun yeni yaprak büyürken, daha önce çıkmış olan yapraklardan uzak yönde yoğunlaşır. Örneğin ikinci yaprak çıkarken önce büyüme hormonu birinci yapraktan en uzak bölgede (180⁰) yoğunlaşmaya başlayacak; ikinci yaprak büyürken ardından üçüncü yaprak çıkmaya başlayacak ve ikinciyi büyüten hormonu biraz (ama biraz, çünkü üçüncü yaprak henüz birinciden çok küçük) daha ileriye itecektir. Bu durumda ikinci yaprak, birinciye göre 180⁰’den daha büyük bir açıyla (Şekil – 9’da 222,5⁰) yerleşecektir[vi]. 

Kar kristallerinin büyümesi konusunda değindiğimiz gibi bu spirallerin oluşup büyümesinin analizi ve açıların değerlerinin belirlenmesi ayrıntılı bilgisayar modelleriyle yapılıyor. Burada yalnızca yaklaşık bir fikir vermek istenip konunun ayrıntısına girilmedi.

SONUÇ

Bu kısa incelemede bazı büyüme süreçlerinde gözlediğimiz büyüleyici biçimlere, kar kristallerine ve spiral yapılara değindik. Bunları incelemek “ne işe yarar” denebilir. Ama sanırım yalnızca “anlamak” bile büyük bir haz veriyor. Değindiğimiz örneklerin dışında hayret ve hayranlık uyandıran sayısız ilginç doğa olayı var. Bu gibi olayları farklı yöntemlerle yorumlayabiliriz.

·         Örneğin “Yaradan öyle yaratmış” diyerek susabiliriz. Böylece kolaycılığa kaçıp daha ötesini incelemekten kurtuluruz. Bu durumda “Dünya mı Güneşin çevresinde dönüyor; yoksa Güneş mi Dünyanın?” bizim için önemi yoktur.

·         Diğer yandan açıklamakta zorlandığımız doğa olaylarına bilimsel yöntemle bakıp bulgularımızı soyutlayarak matematiksel biçimde ifade edebiliriz. 

Bu farklı yaklaşımların farklı sonuçları olacaktır. “Faydacı” bir bakış açısıyla değerlendirirsek ikinci yaklaşımla örneğin Güneş sisteminin düzenini anlayıp gezegenlere uydu gönderebiliriz. Elektrik ve manyetik kuvvetleri inceleyip radyo, televizyon internet ağları kurabiliriz. DNA yapısını çalışıp genlere dayalı tıp yöntemleri geliştirebiliriz.

Diğer yandan Galileo Galilei (1564 – 1642) teleskobunu gökyüzüne çevirirken doğayı merak ediyor ve anlamak istiyordu. Her halde Mars’a gitmeyi düşünmüyordu. Heinrich Hertz (1857  - 1894) elektromanyetik dalgaları incelerken interneti hayal etmiyor; Gregor Mendel (1822 – 1884) bezelyeler üzerinde deneyler yapıp kalıtımı gözlerken, genler üzerinde işlemler yaparak hastalıkları tedavi etmeği amaçlamıyordu. Bilimin temelinde merak, anlama isteği yatıyor. Bu merakı gidermek için de tek yol bilimsel yöntemin uygulanması.

Eğer ülkemizin ortaçağ karanlığına yönelmesini değil çağdaş uygarlıkta yer almasını istiyorsak öncelikle içimizdeki merak ve anlama isteğinin geliştirilmesi, tüm eğitim aşamalarında amaçlarımızdan biri olması ve temel bir kişilik özelliğimiz haline gelmesi sağlanmalıdır. İkinci boyut da yine eğitim sistemimizde bilimsel yöntemin öğretilmesi ve özümsenmesi olmalıdır. 

A. Einstein’in ünlü sözü ile tamamlayalım: “Dünya hakkındaki en kavranamaz şey, onun kavranabilir olmasıdır”[vii] .

NOT: Bu yazı 26 Nisan 2017 Tarihinde Cumhuriyet Gazetesinin Akademi ekinde yayınlandı.

---

[i] Augustus De Morgan, “A Budget of Paradoxes” Longmans, Green, and Co.: Londra: (1872).

[ii] Kenneth Libbrecht ve Rachel Wing, “The Snowflake: Winter's Frozen Artistry”, Voyageur Press: Minneapolis (2015).

[iii] http://www.snowcrystals.com/morphology/morphology.html

[iv] Leonardo Fibonacci, Liber Abaci - Hesaplama Kitabı - (1202)

[v] Bu ϕ sayısı resim, heykel, mimari gibi sanatlarda çok kullanılan ve bunlardaki güzelliği oluşturan altın oranı da verir. 

[vi] Burada yalnızca spiralleri oluşturan bir büyüme modeli ele alındı. Kuşkusuz daha başka modeller de var. Örneğin mısır sapında olduğu gibi ikinci yaprak büyürken üçüncü gelmezse ikinci yaprak 180⁰’ye yerleşebilir ve spiral oluşmaz.

[vii] Antonina Vallentin, “Einstein: A Biography”, s. 24, Weidenfeld and Nicolson Ltd.: Londra (1954).