Bir öneki yazımda 19.
Yüzyıl sonunda, 20. Yüzyıl başında bilim alanında o zamana dek geliştirilmiş
kuramlarla uyuşmayan bazı deney sonuçları gözlendiğini belirtmiştim. Bu
kapsamda özellikle “Michelson – Morley” ve “Kara Kutu Isıl Işıma” deneylerinin
açıklanamayan sonuçlarını vurgulamıştım. Şimdi 20. Yüzyılda bu bilmecelere
yanıt olarak geliştirilen kuramları ele almaya çalışacağım.
ÖZEL GÖRECELİK KURAMI (Special Theory of Relativity)
Öncelikle bu bölümde ele
alacağımız hareketlerin ivmelenmenin olmadığı sabit ve doğrusal hareketler olduğunu
belirtmeliyim. Fizik terimlerini kullanırsam “ivmelenmenin olmadığı sabit ve
doğrusal hareket eden çerçeveler “eylemsiz referans çerçevesi” (inertial reference frame) olarak tanımlanır:
A ve B eylemsiz referans
çerçeveleri ise B’ye göre A çerçevesi V hızıyla sağa doğru hareket ediyor; A’ya
göre de B çerçevesi V hızıyla sola doğru hareket ediyor.
Albert Einstein
(1879-1955) 1905 yılında "On the
Electrodynamics of Moving Bodies" adlı makalesini yazdı ve "özel
görecelik kuramı" olarak bilinen kuramını oluşturdu. (1916'da konuyu
geliştirerek "genel görecelik kuramını" oluşturacak). Aslında özel
görecelik kuramının anlaşılması hiç de zor değil. Ama çok zor olan bu kuramın
sonuçlarının özümsenmesidir. Ben de kolay olandan başlamak istiyorum.
Kuram aslında iki temel önermeye
(postulat, belit) dayanıyor.
1 ) Hangi cismin (veya
kimin) hareketli, hangi cismin (veya kimin) sabit olduğuna ilişkin öncelikli
bir konum yoktur. (Farklı eylemsiz referans çerçevesindeki gözlemciler kendilerine
göre gözlem yapar),
2) Işığın boşluktaki hızı
(c) sabittir. (Bu yukarıda değindiğimiz Michelson - Morley gibi bir dizi
deneyin sonucundan başka bir şey değil.)
Birinci temel önermeyi tek
başına kabul etmek oldukça kolaydır. Örneğin Vr hızıyla giden bir
roketteki adamın (kendine göre) Vt hızıya bir top
attığını düşünelim. Yerdeki gözlemciye göre
top Vr+Vt hızıyla gidecektir.
Zorluk iki temel
önermenin birlikte ele alınmasıyla başlayacak. Şimdi de roketteki adamın top
atmayıp bir cep feneri yaktığını düşünelim. İkinci temel önermeye dayanarak hem
roketteki adamın hem de yerdekinin ışık hızını aynı "c" olarak
ölçmesi gerekecek!
Oldukça basit bir çarpan
ekleyerek bu sorunu matematiksel olarak çözebiliriz. Hız uzunluk/zaman olduğuna
göre uzunluk ve zamanın değişimi bu konuda anahtar olacaktır.
B eylemsiz referans
çerçevesi A’ya göre v hızıyla hareket ediyorsa B’de L0 uzunluğunda ölçülen cetvel A’daki gözlemci için Lv uzunluğundadır:
Benzer biçimde B’de T0 olarak ölçülen zaman, A’ya
göre Tv kadardır:
(Bu formüllerin
çıkartılmasına girmeyeceğim, ama yapılarının oldukça basit olduğuna, v hızının
c’ye göre çok küçük olduğu değerler için A ve B’de yapılan gözlemlerin
birbirine yakın olduğuna; farklılığın v’nin c’ye yaklaşması ile oluştuğuna
dikkat edebiliriz)
Yukarıda belirttiğim gibi
soruyu matematiksel olarak yanıtlamamız oldukça kolay, ama kavram olarak kabul
etmemiz çok zor. Bir sopayı fırlattığımızı düşünelim. Hızla havada uçarken
üzerine binip boyunu ölçmemiz olanaksız, ama ölçebilsek, boyu yerdeki durağan
halinden faklı olacak! Veya ikiz kardeşlerden birini uzaya göndersek, uzaydaki
diğerinden daha genç kalacak! Bu örneklerde özümsememizi zorlaştıran konu
uzunluk ve zamanı değişmez, mutlak (absolute)
olarak kabul etmemiz. Uzunluğun ve zamanın bir değişkene (bu önekte hıza) bağlı
olarak değişebileceğini düşünemiyoruz. Paradoks, gerçek ile gerçeğin nasıl
olması gerektiğine ilişkin inancımız arasındaki çelişkidir. Uzunluk ve zamanın
mutlak olması gerektiğine inanıyoruz, ama gerçek bu değil.
Yukarıdaki formüllerde
görülebileceği gibi kısaca hız veya hareket diye ansak da söz konusu hız, ışık
hızı (saniyede 300 000 km) ile karşılaştırılacak bir hızdır. Böyle bir hızla
günlük yaşamımızda karşılaşmadığımızı, uzunluk ve zamanın hıza göre değişimini
hiç gözlemediğimizi belirtmeliyiz. Astronomik ölçümler yapan ve bazı sorunlar
gözleyenlerin dışındakiler de binlerce yıl -çok haklı olarak- güneşin ve
yıldızların yeryüzünün çevresinde döndüğünü düşünmüşlerdi!
Pekiyi, bu ilginç deneysel gözlemin nedeni nedir? Bu konuda da nedenin değil nasılın peşinde olduğumuzu hatırlayıp “yaşadığımız evrenin özelliği böyle” demekten başka bir şey gelmiyor
elimizden (David Mermin, "Space and
Time in Special Relativity" ).
Eğer değişmez, mutlak bir
şeyler bularak kendimizi daha rahat hissedeceksek uzay-zaman (spacetime) kavramına başvurabiliriz. Einstein
Özel Görecelik hakkındaki kuramını oluşturduktan hemen sonra, Einstein’ın
matematik hocalarından biri, Hermann Minkowsky (1864 - 1909), bu kuramı başka bir
açıdan ele alarak uzay-zaman aralığının değişmezliği (invariance of spacetime interval) kavramını geliştirdi. Minkowsky’in
bu çalışması da bu kısa blog yazısının çerçevesi dışında kalıyor. Ama kısaca bir
hareketi iki farklı eylemsiz referans çerçevesinde gözlediğimizde, bu
çerçevelerin her birindeki uzay-zaman koordinat sistemlerinde birer aralık
oluşturacaktır. Bu iki sisteme Lorentz Dönüşümü (Lorentz transformation) uyguladığımızda bu aralıkların ayni
olduğunu görürüz.
Birçok kişi “görecelik kuramına göre her şey görecedir”
diye düşünür. Evet, zaman, uzunluk ve eşzamanlılık gözlemin yapıldığı çerçeveye
göre değişir. Ama ışık hızı ve uzay-zaman aralığı sabit kalır.
Michelson – Morley deney
sonuçlarının dönemin fizikçilerini şaşırtması hareket konusunda –ışık hızına yakın
hızlarda bile- Newton hareket
yasalarının geçerli olduğuna inanmalarından kaynaklanıyordu. Özel görecelik kuramında
ışık hızının değişmez olması öngörüldüğüne göre Michelson – Morley deneyinin
verdiği sonuç hiç de şaşırtıcı değildir.
GENEL GÖRECELİK KURAMI (General Theory of Relativity)
Bekleneceği gibi Einstein
bu özel kuramı genel hale getirmek için hemen çalışmaya başladı. Ama sınırlayıcı
varsayımlardan kurtarmak, hareketin içine kütleçekim kuvvetinin etkilerini
katmak ve bunları ifade eden denklemleri kurmak yıllar süren bir çalışma
gerektiriyordu. Sonunda Einstein 1916’da yayımladığı “The Foundation of General Theory of Relativity” başlıklı makale ile
Genel Görecelik Kuramını tanımladı.
Genel Görecelik Kuramı da
iki temel önermeye (postulat, belit)
dayanıyor.
1) Genel Ortak Değişinti
(General Covariance) (Covariance - iki değişkenin ne kadar birlikte
değiştiklerinin ölçüsü)
2) Eşdeğerlik (Equavalence)
Hatırlayacağınız gibi
özel görecelik kuramı tartışmasına başlarken ele alınacak hareketlerin çerçevelerinin
“eylemsiz” (ivmelenmenin olmadığı sabit ve doğrusal bir hareket) olduğunu
belirtmiştim. Ortak değişinti temel önermesi ise bu “eylemsizlik” koşulunu kaldıran
bir anlatımla “Fizik yasaları bütün
referans çerçevelerinde aynıdır” şeklinde özetlenebilir.
Eşdeğerlik temel önermesi
ise “hareket ivmesinin ve kütleçekimin
gözlenen etkileri ayıt edilemez” şeklinde özetlenebilir. Bu konuda Einstein
bir asansör benzeri bir oda örneği veriyor. İlk olarak dışarısını göremediğimiz
yeryüzünde bir oda içinde olduğumuzu düşünelim. Bedenimizin kütleçekim ile
odanın tabanına çekildiğini, bıraktığımız bir cismin yere düştüğünü gözleriz.
İkinci olarak odanın uzayın uzak bir bölgesine taşındığını, dolayısıyla
herhangi bir kütleçekim kuvvetinin etkisi olmadığını düşünelim. Uzaydaki bu
odanın yerkürenin neden olduğu kütleçekimine eşit bir ivme (9,8 m/s2 )
ile hareket ettirildiğini düşünelim. Odadaki gözlemci yine bedeninin odanın
tabanına doğru çekildiğini ve bıraktığı cisimlerin yere düştüğünü
görecektir. Eşdeğerlik temel önermesine
göre bu iki durumda gözlenenler ayırt edilemez.
Aslında kütleçekim kuvveti
ve ivme çok daha önceleri incelenmişti. Galileo’nun ünlü söylencede Pisa
kulesindeki kütleçekim deneylerini, ivme ile kuvvet arasındaki ilişkiyi F=m*a olarak belirleyen Newton’u hatırlayalım.
Ama 20. Yüzyıl başına kadar bu iki olay arasında ilişki kurulamamıştı. Genel
Görecelik Kuramında bu ilişki kuruldu ve o zamana dek kuramsal olarak
açıklanamayan bir dizi nasıl
açıklandı.
Özel Görecelik Kuramında
temel önermelerden yola çıkarak uzunluk ve zamana ilişkin denklemlerine
ulaşmanın oldukça basit olduğunu belirtmiş ve örneklerini yukarıda vermiştim.
Genel Görecelik Kuramında ise denklemlere ulaşmak çok karmaşık fizik ve
matematik işlemleri gerekmektedir. Bu konuda Einstein’in esprili ifadesi
anılabilir “Nedense herkes beni seviyor
ama hiç kimse beni anlamıyor” (New York Times, 12 Mart 1944). Biz de bu karmaşık denklemleri ele almak
yerine kurama ilişkin birkaç gözlemi sıralayalım.
Einstein’ın Genel
Görecelik Kuramı birçok açıdan geçerli fizik kuramlarını sarsıyordu. Kuramın
doğruluğu konusunda ilk gözlem 1919 Mayıs ayındaki güneş tutulması sırasında
yapıldı ve güneş kütlesinin bir yıldızdan gelen ışığı tam da Einstein kuramının
öngördüğü biçimde büktüğü gözlendi.
Bir önceki bölümde
bilmeceleri sıralarken Merkür’ün yörüngesinde güneşe en yakın noktanın (perihelion) güneş çevresindeki yörünge üzerinde kaydığını
belirtmiştim. Genel Görecelik Kuramının denklemleri bu olayı da tam olarak
açıklıyordu.
Genel Görecelik Kuramı
büyük bir kütleden uzaklaşan ışığın frekansının kırmızıya doğru kayacağını
öngörüyordu (gravitational redshift).
Bu kayma genel bir olgu olarak yıllardır beklense de kaymanın büyüklüğü
hesaplanamıyordu. 1919’da güneş tutulması sırasında yapılan gözlemler
kütleçekim kırmızıya kayması büyüklüğünün Einstein denklemlerinde hesaplandığı
kadar olduğunu gösterdi.
Fizik derslerimizde
manyetik alanlar için yandaki resimde gördüğümüz gibi bazı deneyler ve çizimler
hatırlarız. Burada mıknatısın kutupları yakınında alanın daha şiddetli olması
daha sık çizgilerle, uzaklardaki alanın daha az şiddetli olması daha seyrek
çizgilerle gösterilirdi.
Eğer benzer bir uygulamayı kütleçekim alanı
çizgilerini uzay-zaman üzerinde için düşünürsek aşağıdaki gibi bir şekil
çizebiliriz:
Burada da sıklaşan
çizgiler kütleçekim kuvvetinin büyümesini gösteriyor. Hatta uzay-zamanın büyük
bir kütlenin varlığı ile büküldüğünü ve büyük kütlenin bir çukur oluşturduğunu
düşünebiliriz:
1960’ların sonunda
gökyüzünde ışığın bile “kaçamadığı” karadeliklerin gözlendiğinin kesinleşmesi,
nihayet 2015 sonbaharında kütleçekim dalgalarının gözlenmesi Genel Görecelik
Kuramının gözlemlerle doğrulandığı önemli olaylar olarak belirtilebilir.
Son olarak uzay-zamanın
büyük kütleler etkisiyle bükülmesi kavramının bizi düşünsel olarak Newton
fiziğinden çok farklı bir yere götürdüğünü vurgulayalım. Artık bir kütleçekim
kuvveti ve gezegenlerin bu kuvvetin etkisi altında –örneğin- güneş çevresinde
döndüklerini varsaymak zorunda değiliz. Gezegenlerin düz gittiklerini, ama
uzay-zamanın bükülmesi nedeniyle büyük kütlenin çevresinde dönüyormuş gibi
gözlendiğini düşünebiliriz. Dikkat edilirse
bu düşünce biçimi insanlığın Aristo’dan Newton’a geçerken yaptığı gibi
devrimsel bir değişikliktir.



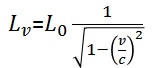




Hiç yorum yok:
Yorum Gönder